Latent Dirichlet Allocation

• Blei, D. M., Ng, A. Y., & Jordan, M. I. (2003). Latent dirichlet allocation. Journal of machine Learning research, 3(Jan), 993-1022.

• Python: sklearn.decomposition.LatentDirichletAllocation.

1. Summary

This paper presents a generative probabilistic model for collections of discrete data such as text corpora. LDA is a three-level hierarchical Bayesian model with topics as latent variable. The parameter estimation and inference tasks can be made via a combination of variational method and EM algorithm.

2. Structure

We define:

• A word is the basic unit of discrete data, defined to be an item from a vocabulary indexed by $\{1, .\ldots , V \}$. We encode words with one-hot coding.
• A document is a sequence of $N$ words denoted by $\mathbf{w} = (w_1,w_2, \ldots ,w_N)$, where $w_n$ is the $n$th word in the sequence.
• A corpus is a collection of $M$ documents denoted by $\mathbf{D} = \{\mathbf{w}_1, \mathbf{w}_2, \ldots , \mathbf{w}_M\}$.

LDA assumes the following generative process for each document $\mathbf{w}$ in a corpus $\mathbf{D}$:

1. Choose $N \sim \operatorname{Poisson}(\xi)$.
2. Choose $\theta \sim \operatorname{Dir}(\alpha)$. The dimension of this Dirichlet distribution is assumed known and fixed.
3. For each of the $N$ words $w_n$: (a) Choose a topic $z_{n} \sim \text { Multinomial }(\theta)$. (b) Choose a word $w_n$ from $p\left(w_{n} | z_{n}, \beta\right)$, a multinomial probability conditioned on the topic $z_n$.

Basically, we allocate the multinomial probability of $k$ latent topics using hyper-parameter $\alpha$ and then sample each word from the sampled multinomial distribution.

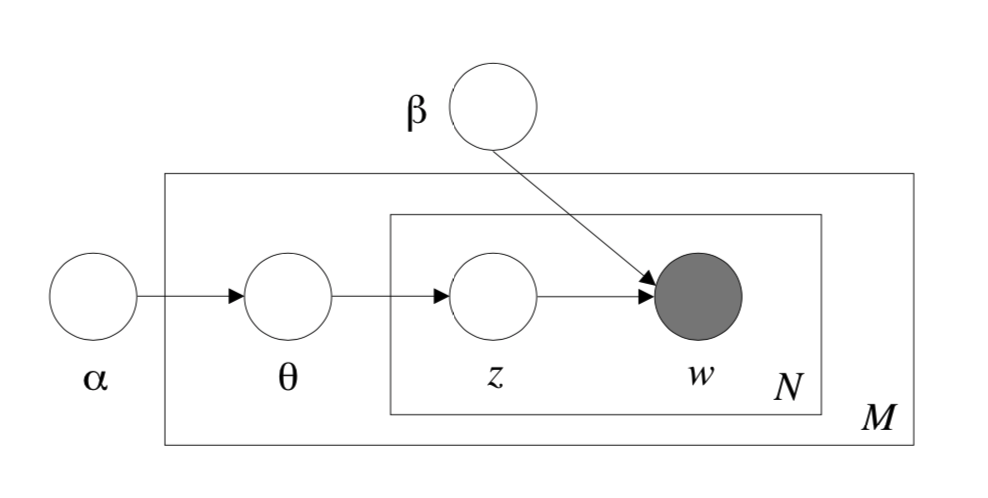Figure 1: Graphical model representation of LDA. The boxes are "plates" representing replicates. The outer plate represents documents, while the inner plate represents the repeated choice of topics and words within a document.

Therefore, we can obtain the marginal distribution of a document:

$$p(\mathbf{w} | \alpha, \beta)=\int p(\theta | \alpha)\left(\prod_{n=1}^{N} \sum_{z_{n}} p\left(z_{n} | \theta\right) p\left(w_{n} | z_{n}, \beta\right)\right) d \theta$$

The probability of a corpus given parameter $\alpha, \beta$ is

$$p(\mathbf{D} | \alpha, \beta) =\prod_{d=1}^{M} \int p\left(\theta_{d} | \alpha\right)\left(\prod_{n=1}^{N_{d}} \sum_{z_{d n}} p\left(z_{d n} | \theta_{d}\right) p\left(w_{d n} | z_{d n}, \beta\right)\right) d \theta_{d}$$

3. Learning and Inference

The key inferential problem that we need to solve in order to use LDA is that of computing the posterior distribution of the hidden variables given a document:

$$p(\theta, \mathbf{z} | \mathbf{w}, \alpha, \beta)=\frac{p(\theta, \mathbf{z}, \mathbf{w} | \alpha, \beta)}{p(\mathbf{w} | \alpha, \beta)}$$

which is intractable because of the intractability of $p(\mathbf{w} | \alpha, \beta)$. We consider using a variational inference method to approximate this posterior distribution:

$$q(\theta, \mathbf{z} | \gamma, \phi)=q(\theta | \gamma) \prod_{n=1}^{N} q\left(z_{n} | \phi_{n}\right)$$

As for the learning task, we wish to find parameters $\alpha$ and $\beta$ that maximize the (marginal) log likelihood of the data:

$$\ell(\alpha, \beta)=\sum_{d=1}^{M} \log p\left(\mathbf{w}_{d} | \alpha, \beta\right)$$

since $p(\mathbf{w} | \alpha, \beta)$ is intractable, We can thus find approximate empirical Bayes estimates for the LDA model via an alternating variational EM procedure that maximizes a lower bound with respect to the variational parameters $\gamma$ and $\phi$, and then, for fixed values of the variational parameters, maximizes the lower bound with respect to the model parameters $\alpha$ and $\beta$:

1. (E-step) For each document, find the optimizing values of the variational parameters $\left\{\gamma_{d}^{*}, \phi_{d}^{*} :d \in \mathbf{D} \right\}$. This minimization can be achieved via an iterative fixed-point method.

$$\left(\gamma^{*}, \phi^{*}\right)=\arg \min _{(\gamma, \phi)} \mathrm{D}(q(\theta, \mathbf{z} | \gamma, \phi) \| p(\theta, \mathbf{z} | \mathbf{w}, \alpha, \beta))$$

1. (M-step) Maximize the resulting lower bound on the log likelihood with respect to the model parameters $\alpha$ and $\beta$. This corresponds to finding maximum likelihood estimates with expected sufficient statistics for each document under the approximate posterior which is computed in the E-step.